Posts

Analogies in Planning using Functorial Data Migrations

planning

c-sets

data migrations

What if I told you to walk on the floor like it was lava? Or pull out Tupperware like its a Jenga tower? How would you plan your next move?

Angeline Aguinaldo

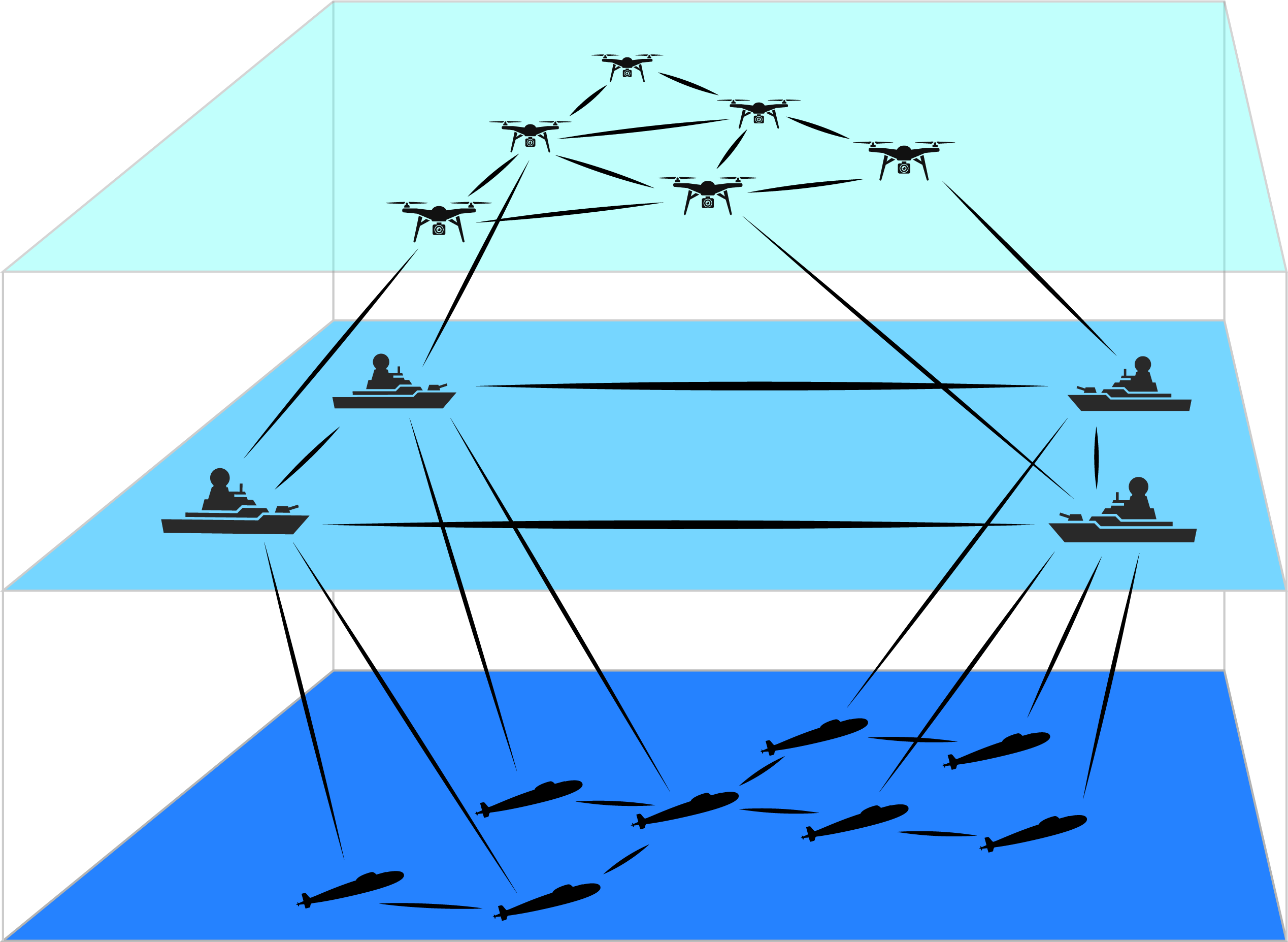
Multi-agent Coordination with AlgebraicJulia using Cellular Sheaves

dynamical systems

optimization

planning

How can we model and solve multi-agent coordination problems in AlgebraicJulia?

Tree Decompositions in Julia

graphs

CliqueTrees.jl is a Julia package for computing tree decompositions and chordal extensions of graphs.

Richard Samuelson

JuMP-ing with AlgebraicJulia II: A practical optimization model

optimization

visualization

Looking at using ACSets to structure and solve a fundamental network optimization model.

Catlab refactor II: Basic Sets

code

Examples of theories and models for sets and functions in Catlab.jl.

Catlab Refactor I: GATlab Preliminaries

GATs

logic

An introduction to some big upcoming changes in Catlab, with a focus on GATlab.jl.

JuMP-ing with AlgebraicJulia I: The IJKLM model

algebra

logic

optimization

How can we tackle relational algebra of the sort seen in optimization models using tools from AlgebraicJulia?

Introducing InterTypes

attributed-c-sets

integration

Announcing the first version of InterTypes: a package for cross-language serialization for ADTs and ACSets

Agent-based modeling via graph rewriting

rewriting

attributed-c-sets

models

dynamical systems

Rewrite rules are organized via a graphical syntax into discrete-time simulations which can be understood as agent-based models. This representation is transparent, compositional, and serializable.

Acsets with variables

algebra

logic

Acsets are great, but what if attributes could be variables?

Kevin Arlin, Kris Brown

Symbolic presentations of dynamical systems

algebra

logic

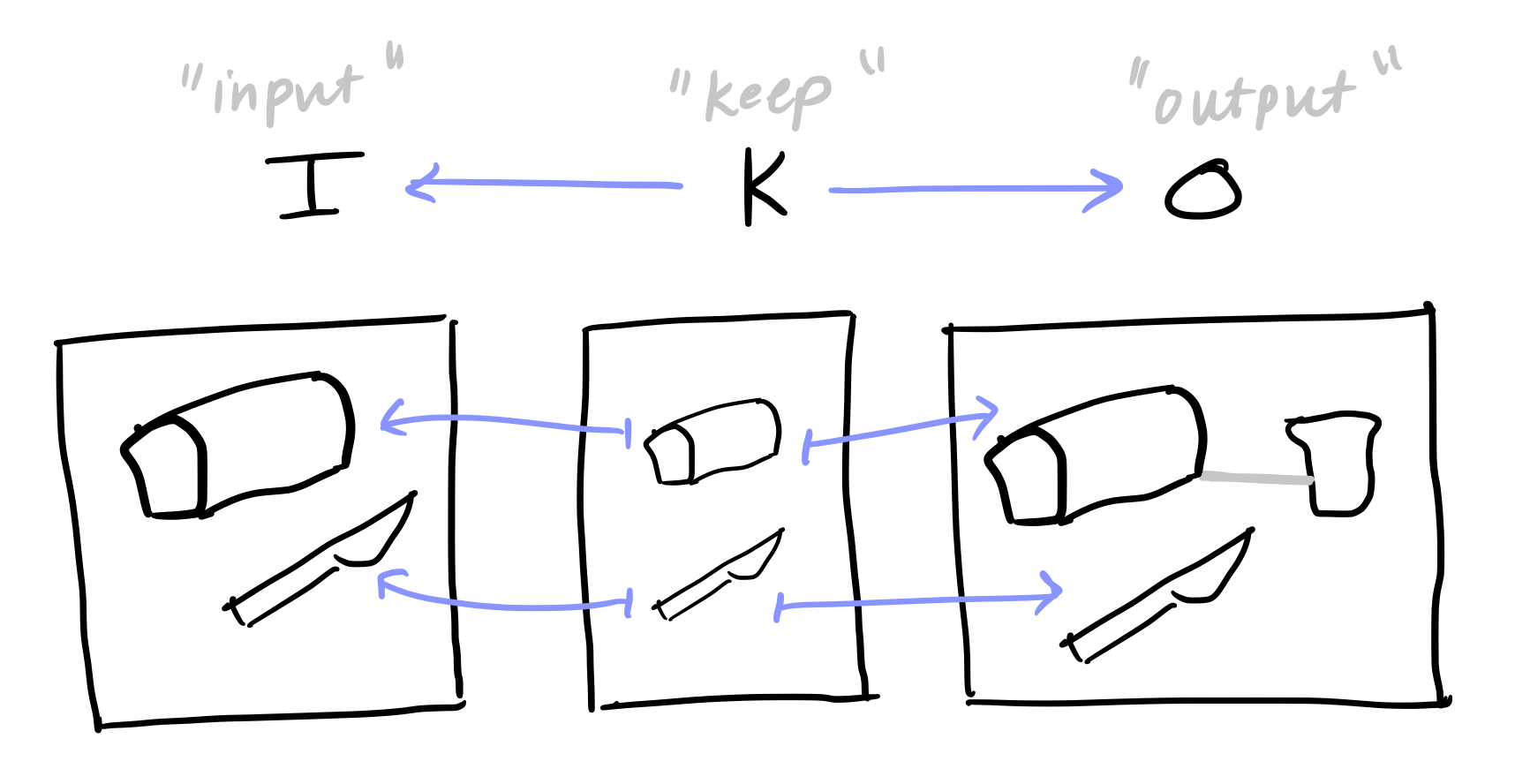
A follow-up to Algebraic Geometry for the Working Programmer, this post explains a category-theoretic approach to symbolic open dynamical systems.

Algebraic geometry for the working programmer

algebra

logic

In this series of posts, we investigate the duality between algebra and geometry in order to develop new types of lenses. In this first post, we review some basic ideas about algebraic geometry that will be needed in the coming posts.

Using categorical logic for AI planning

planning

rewriting

c-sets

It’s breakfast time! You wake up and walk to your kitchen and notice a loaf of bread, a knife, a raw egg (in its shell), a skillet, and a stove burner sitting on the counter. You’re hungry and your preferred state of existence is to, instead, have an egg sandwich sitting on your counter. You are saddened by the situation, but feel empowered to change it! You compare what you have and what you want, recall what cooking skills you have, and devise the following steps:

Angeline Aguinaldo

The chase: data repair and logical reasoning

c-sets

databases

logic

The chase in an algorithm in the context of databases that has applications in Catlab for model exploration, term rewriting, and enforcing schema axioms.

Equality vs equivalence: computing isomorphism classes of C-sets

c-sets

attributed-c-sets

databases

For graphs and C-sets more generally, the most useful notion of equivalence differs from strict equality of the underlying data structures. Finding automorphism classes of C-sets addresses this problem; we explore how to compute automorphism classes and applications of them.

Graphs and C-sets IV: The propositional logic of subgraphs and sub-C-sets

c-sets

graphs

logic

Nonclassical logics are often thought to be abstruse and exotic, but they arise naturally as the logic of connected spaces. In this post, we introduce the propositional logic of subgraphs, and more generally of sub-C-sets, and illustrate it with computational examples. The nonclassicality of this logic is seen to be not just natural but inevitable, and also surprisingly useful.

David Jaz Myers and Evan Patterson

Graphs and C-sets III: Reflexive graphs and C-set homomorphisms

c-sets

graphs

Reflexive graphs are graphs where every vertex has a distinguished self-loop. While this may seem inconsequential, reflexive graphs have interestingly different properties than ordinary graphs owing to their different morphisms. We will see that reflexive graphs are more geometrical than graphs and also review the general notion of homomorphism between C-sets.

Composing open dynamical systems II: Undirected composition

models

attributed-c-sets

dynamical systems

In the previous post, we defined a general approach for composing dynamical systems based on the mathematics of operads and operad algebras. In this post, we explore an undirected composition syntax in which dynamical systems compose by sharing resources. We also get a taste of hierarchical composition, i.e. composing systems which are themselves composites.

Sophie Libkind and James Fairbanks

Composing open dynamical systems I: Directed composition

models

attributed-c-sets

dynamical systems

Informally, many models are specified as compositions of primitive dynamical systems. In this series of posts, we make this modular specification formal by introducing a computing framework from composing open dynamical systems. In this first post of the series, we examine directed theories for composition.

Sophie Libkind and James Fairbanks

C-sets for data analysis: relational data and conjunctive queries

databases

c-sets

attributed-c-sets

Not just useful for graphs, C-sets are a general-purpose tool for data analysis offering the functionality of an in-memory relational database. In this post, we illustrate Catlab’s new capabilities for querying C-sets and we explain the categorical underpinnings of conjunctive queries.

Compositional epidemiological modeling using structured cospans, part 2

structured cospans

operads

models

Following up the original post, we explain how modeling is simplified by a shift in perspective from composing structured cospans in categorical style to composing structured multicospans in operadic style.

Micah Halter and Evan Patterson

A categorical approach to scientific data management

databases

workflow

attributed-c-sets

We present an approach to scientific data management that utilizes category theory to seamlessly integrate workflow creation, database generation, and database querying. We use Catlab as a backend to provide this more continuous and consistent database experience.

Compositional epidemiological modeling using structured cospans

structured cospans

c-sets

models

Structured cospans are a categorical method for turning closed systems into open ones. We show how structured cospans of Petri nets can be used to construct complex epidemiological models in a compositional way.

Micah Halter and Evan Patterson

The categorical scoop on attributed C-sets

c-sets

attributed-c-sets

In this post we unveil the category of attributed C-sets. It is an upgrade to the category of C-sets that makes each element of a component set (e.g. each vertex or edge in a graph) have attributes, which may be elements of arbitrary sets/Julia types. In order to formalize attributed C-sets, we also take a tour of double category theory and profunctors.

Graphs and C-sets II: Half-edges and rotation systems

c-sets

graphs

Graphs are made up of vertices and edges, but an important variation on this concept is based on “half-edges” or “darts.” We explain how half-edge graphs are implemented as C-sets in Catlab.jl and how they are used in topological graph theory to represent embeddings of graphs in surfaces.

Modeling frameworks: What is a scientific model?

models

logic

What is a scientific model? This post considers how mathematical logic and category theory can help us understand scientific models, and how AlgebraicJulia aims to build modeling frameworks based on this understanding.

James Fairbanks

On the implementation of C-sets

c-sets

graphs

The idea of a C-set was introduced in an earlier post. In this post, we explain how C-sets are implemented as a data structure in the Julia programming language.

Graphs and C-sets I: What is a graph?

c-sets

graphs

Through the course of this blog we will encounter a diverse cast of algebraic structures generalizing the concept of a graph. In this post we start at the very beginning, with how category theorists understand graphs, how graphs are an example of a general class of structures called “C-sets,” and how C-sets can be used as data structures in Julia through Catlab.jl.