Posts
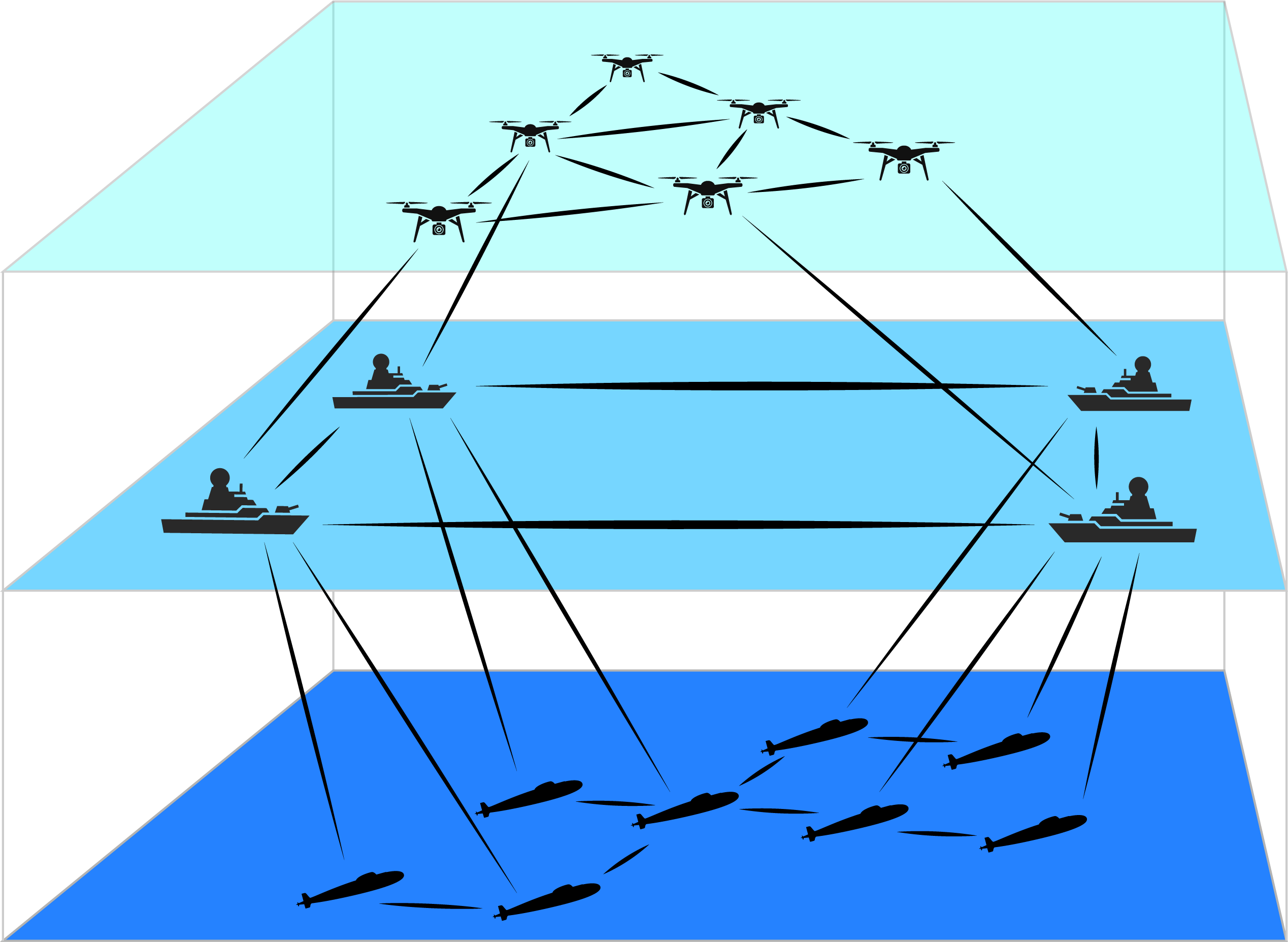
Multi-agent Coordination with AlgebraicJulia using Cellular Sheaves
dynamical systems
optimization
planning
Symbolic presentations of dynamical systems
algebra
logic
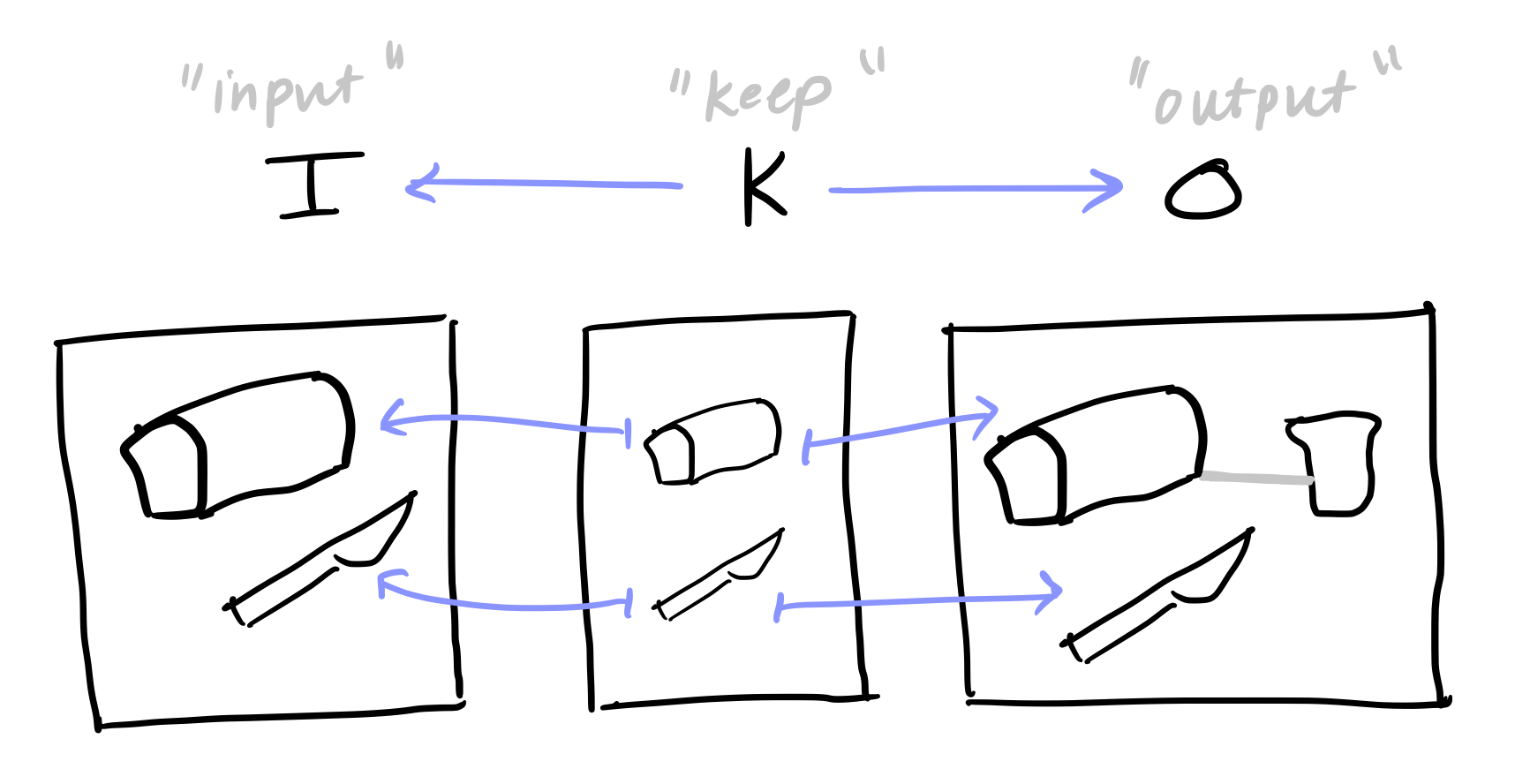
A follow-up to Algebraic Geometry for the Working Programmer, this post explains a category-theoretic approach to symbolic open dynamical systems.
Using categorical logic for AI planning
planning
rewriting
c-sets
Equality vs equivalence: computing isomorphism classes of C-sets
c-sets
attributed-c-sets
databases
Graphs and C-sets IV: The propositional logic of subgraphs and sub-C-sets
c-sets
graphs
logic
Composing open dynamical systems II: Undirected composition
models
attributed-c-sets
dynamical systems
Composing open dynamical systems I: Directed composition
models
attributed-c-sets
dynamical systems
C-sets for data analysis: relational data and conjunctive queries
databases
c-sets
attributed-c-sets
Compositional epidemiological modeling using structured cospans, part 2
structured cospans
operads
models
A categorical approach to scientific data management
databases
workflow
attributed-c-sets
Compositional epidemiological modeling using structured cospans
structured cospans
c-sets
models
The categorical scoop on attributed C-sets
c-sets
attributed-c-sets
Graphs and C-sets II: Half-edges and rotation systems
c-sets
graphs
Graphs and C-sets I: What is a graph?
c-sets
graphs
No matching items